Session 1: 9/08/2016 Defining an Additive Thinker
Resource: The Numeracy Project
Children struggle to make the cross over with everyday life.
Maths is about being flexible with numbers. It involves calculating and estimating, using mental and written strategies.
Book 2 will tell you what the children need to know-pg 15.
- Big ideas should be a starting point - Book 5.
- Put our problems into contexts. Give the children a reason and a purpose for their learning.
- DO LESS BETTER.
Children need to have opportunities to image. This is something that will come when they are ready. If they don't get it, move on.
What is Additive Thinking?
- Combining, joining (addition), splitting, taking away (subtraction) to make a new set.
- Addition and Subtraction are inversely related-family of facts.
- Teach Add/sub at the same time.
Children need to be exposed to bigger numbers. This gives them the opportunity to think about patterns.
Questioning
Book 5-pg 7. Good examples of questions to ask - open ended.
- What operation do we need to use to solve this problem?
- How will we record what we have just done with the equipment?
- What symbol should we use when we are finding the difference between two amounts?
- Are there two ways we could record this problem?
- Can anyone write a new problem that will work for this strategy?
Equals Sign
Means balance.
"is the same as."
Vary representations: J=3 + 2
New names for numbers: 3 + 4 = 6 + 1 = 5 + 2
True and false statements.
Book 5 Pg 8 - Different problem types.
What is Part-Whole Thinking?
- Use part-whole thinking as soon as possible.
- More possibilities for children to solve a problem.
- Gives the children the opportunity for different kinds of thinking.
Give Opportunities
Leave off the question of a problem.
Act out the context.
Write the problem with the numbers as words.
What is Place Value
The meaning of an individual digit.
Grouping/place value
Groups within other groups e.g. 1&9, 2&8, 3&7 ....
Grouping images e.g. 10's frame, hundreds board
Structure of numbers and number patterns.
Materials
Caterpillars
5's Frames
10's Frames
Abacus
Numicon
unifix or multilink cues. Have these set up in 5's. Helps children to make connections.
Using these materials builds pictures in children's heads of numbers.
Idea: Use a piece of string. Children have to image it is a number line. They have to find the location of numbers and explain why.
Asking Children CAN YOU PROVE IT?
Place Value: Components
Write it
Say it
Read it
Make it
Draw it
Provides the children with the true meaning of a number.
- Position: The position of a digit in a number indicates its value.
- Base 10 system. Only 10 digits to allow us to create any number and there are patterns in this system.
- Additive-digits in a number are added to give its total value.
- Multiplicative- the value of each digit is multiplied by the value of its place.
What about Zero?
Means nothing
Zero is a place holder.
Introducing Numbers to Children
1. Begin with materials where you can pull the apart and the put them back together.
2. Groups of - Children can't pull them apart.
3. Imaging. Children begin to trust that there are groups of a number.4. This is what we tend to start with.
Common Mistakes
We need to practice the idea of trading.
E.g. 47 = 5. Some children don't understand that they can swap 10 ones for 1 ten to change the 40 to a 50.
Think...Do I?
- Develop and understanding of groups with in groups?
- Spend more time on structure and patterns?
- Delicate time specifically for place value.
Making Connections
- Different ways of solving problems
- mathematical representations
- mathematics to everyday experiences
- prior knowledge to new learning
- big ideas - why? What's the purpose?
- Strategies? Are there similarities? Differences?
Teaching Model
Children should be constantly jumping backwards and forwards by using resources.- Start with a problem - with a context. Make WALTs broader.
- Always have different materials available. They can choose to use these and they can choose what strategy they prefer.
- Think, pair, share, - maths is a social subject.
- Choose one strategy (most common - more people involved).
- If you are giving a worksheet, there must be space for children to show their working.
- You have to train children to talk about their ideas. This can be daunting.
- Children will then reason. Do they agree or disagree. They don't disagree with the person, only their thinking.
- Allow wait time! 10 Seconds!
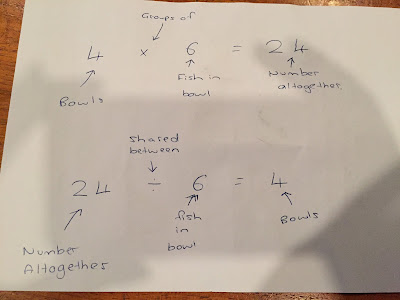
Children need to understand and co-ordinate 3 qualities.
- The whole quality
- The number of equal groups.
- The number in each group.
Stage 5- Children need to know 2, 5, 10 times tables and they are beginning to know 3. They also need to know their division facts.
Skip Counting
"How many feet in the room?" "How many fingers in the room?"
Children need to make connections with... hundreds board, bead string, number line, abacus, pictures.
Children need to do lots of drawing.
It is important for children to draw a set or a group.
 Division is a daunting aspect for children. It is all about sharing. This is easier for children to think about.
Division is a daunting aspect for children. It is all about sharing. This is easier for children to think about.
Equal Groups
Use of dice cards. These are familiar to the children. They should be able to look at them and know exactly how many dots are in the square without counting them.
Examples of use: "Show me three groups of 5. Show me one less group." You could cover a group of these up and children have to guess how many is behind the cover.
Children need to get used to the term 'group of.'
Teaching Multiplicative Thinking
At the counting stages of thinking the size of numbers is restricted. There is normally only one way to solve a problem.
Vocabulary
x means - groups of, lots of, sets of, rows of, times, multiply. The children may not know what all of these mean. It is important to use all of these terms as the children need to know it.
Factors - numbers we can multiply together to get another number. - Stage 6.
Product - the result of 2 numbers multiplied together.
Division - shared equally.
3 x 5 - in New Zealand we read this as 3 groups of 5. In other countries they say 3 replicated 5 times. It is important to be wary of this.
Children need to be able to draw the representation of multiplication. e.g. 2 x 4.
They need an awareness of mathematical patterns and structures.
Why use Arrays?
- Visual
- Make sense of multiplication
- Encourage multiplicative thinking
- Develop a deeper concrete understanding of multiplication
- Helps children to visualise the multiplicative properties.
- Links multiplication to area.
Children will learn about the distributive property - the image of tiles.
(5 x 4 = 20) + (1 x 4 = 4) = 20.
Book 6
Pg 5 - Problem types
Keep this with your planning and tick off as you expose the children to the different problem types. Even juniors can use these.
Only issue with Book 6 is there is not much array work.
Multi-digit Multiplication - Stage 7
To do this children must know place value and their basic facts.
Division
- Equal Shares
- Comparison - " Cassandra picked 24 apples. She picked 4 times as many apples as Betty. How many apples did Betty pick?
- Remainders are important! More often than not division doesn't result in a simple whole number.

Basic Facts
Children need to know all division and multiplication facts.
No timed or rote learning. Leads to anxiety.
Give the children different ways of learning their basic facts.
Helpful resources
ALiM NZ Maths site. Helpful information if you have a child that is stuck and your struggling to get them to move stages.
Study ladder
Homework
Give the children a problem. They work it out their way and have their parents work it out another way. They can talk about the similarities and differences in their strategies.
Follow up Activities
Children need an opportunity to go away and practice a new concept. Only give them one worksheet a week. They need to show their working!
Her Programme
Must Dos and Can Dos.
Must dos- basics facts, 81 + 5 = write some word problems for this equation, I have 12 what could be an equation?
Can dos - Group box. This would have strand activities: measurement, geometry, and fractions.
She would have workshops that the children could opt into. She would say if you want help counting backwards or skip counting come and see me. The children could opt into more than one workshop.
Handy Hints
Practising skip counting. Mix it up. Start at 23 and skip count in 10s. Discuss the importance of adding 10s.
Use of hundreds board - practise skip counting and look for patterns.
Abacus- set up 8 groups of 6. NO SKIP COUNTING. Children will have to add up the 5's.
It is important to show the adding groups.
Show what the equation means.
Word Story
4 x 3 = 12. 3 x 4 = 12. Please do not say that these are the same. Yes the answers are the same but they look very different!
Yolanda Soryl Phonics Course April 2016
This course was very amazing, explained in such detail with examples.
Yolanda first talked about the research related to Phonics. What stood out to me was:
- When teaching phonics, there must be quiet.
- Phonics influences children to think about 4 different aspects of text: the phonics (sounds), context (thinking about the whole story), grammar (thinking about how the reading sounds) and word recognition and graphic knowledge (visually memorise the shape).
- Phonics is proven to be helpful and rises achievement in all children, including those at risk.
- Fluency is very important. To work on this, ask the children to do it again, only faster.
Yolanda then went on to demonstrate and model lessons from Stage 2, 4 and 5. These she modelled them exactly how she would teach them to children. Then she went and talked about each of the things she did and why she did them.
This course was great. I was given a resource that explains all of the Stages in detail, along with the key words and sounds and assessment. I also bought a book - "Developing Phonological Awareness." This is a handbook with all sorts of very short lessons that teaches phonological awareness skills. This will be a great resource for when I have a few spare moments in the classroom to fill with something meaningful.
I walked away from this course felling like I could teach a Phonics lesson with more confidence and with a much more detailed process.
I feel that I need to read up again in the course lesson plans. But I am very excited to teach my first Phonics lesson!
Session 3: Fractions 20/9/16
Fractions is often the most challenging part of Maths. Fractions should be taught first. Children should be exposed to fractions every week.
Some Key Points
Students find it difficult
Teachers find it difficult
It is important to not rely on answers from children. Children can say the correct answer but will not know why that is the answer. Children have to be able to explain why they have that answer.
What are fractions?
They are numbers.
They are found between whole numbers.
Answers to situations where the answer has been partitioned by division.
Equality is important. Equal Sharing.
Discuss the different names for parts, pieces, bits etc.
Discuss the meaning of whole.
If you will use fruit, think about the volume. This can be challenging to find half.
Book 4: Activities on Fractions Pg 17.
Children need to create, see and say fractions.
Teachers jump into symbols too quickly. This doesn't have a lot of meaning for a lot of children. Show them visuals representing the fractions.
Vocabulary
3/4 Top number: Numerator. The counter. Tells you how many of the fraction you have.
Bottom number: Denominator. The namer. Tells you the name of the fraction and how many equal parts there are.
3/4 is not 3 out of 4. It is not 3 over 4.
Use the words not the symbols. By the end of Stage 4 the children need to know the fractions.
Representation Model
Children need to know that 1/5 is 5 spaces on a number line.
Continuous Models
These are where a shape, length, region or object can be split into parts.
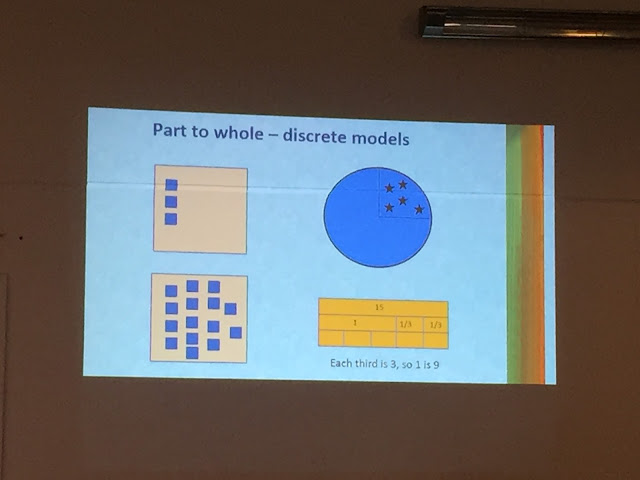
Discrete Models
Made up of individual objects.
Teach children to put these in arrays (lines). This makes counting them a little easier.
1/5, 1/6, 1/7, 1/8, 1/9, 1/10 make more sense to children than half, quarter and third as these relate to the numbers. The first fraction to start with would be 1/8 as this is easier to make.
Squares and rectangles are easier to work with than circles.
Children need to be drawing, making and doing.
Most of the time we give the children a whole and have them cut this into pieces. How often do we give them a piece and say what does the whole look like?
Using a context clarifies things for children. Word problems makes it real and they can relate too real life contexts.
USE WORD PROBLEMS!
Part to Whole - discrete models
Question: "Here is a quarter. What does a whole look like?"
Fractions as Numbers
Teachers could count with fractions and with materials. Count one fifth, 2 fifths, 3 fifths, 4 fifths, 1 whole. 3 fifths plus 3 fifths is 6 fifths. More exposure the language.
Stage 5: Children need to read fractions and they need to understand division and multiplication.
Stage 6:
Children will visualise what fractions look like.
Order unit and common fractions.
Relate these to multiplication.
Understand how fractions relate to place value.
Swimming PD: Kiwi Swim Safe March 2016
Less able swimmers:
- Began with children sitting on side with their bottoms closest to the edge.
- Hard and loud kicks.
- Soft quiet kicks: Helps you not to use your voice as much. The children are told to have long legs. They don't point their toes. They shake their feet.
- Then they rolled on their tummies lying down. Long loose legs. Quiet kicks.
- Slide in quietly, no screaming!
- Bottoms on the bottom of the pool. Go!
- Run to the end.
- Jumping race back-this a time for the children to have fun. Spend this time watching for water confidence.
- Floating on front: Alphabet game. Make a X, Y, I.
- Do you I with some quiet kicking. The children can be a crocodile or a turtle with their hands. They must keep their arms straight and up. Keep their arms covering their ears or they will fall off and then we will have all of these ears at the bottom of the pool. We don't want that.
- The instructor had the boys going first, then the boys.
- Ended with the children showing the instructor their favourite way of swimming.
Non-Swimmers
- Have them practice blowing bubbles inside a hoop. This gives them their own space of water. Makes it a less daunting task for them.
More Able Swimmers:
- Same beginning steps.
- When lying on their back floating, put up their chin then put up tummy and then put up their smelly old feet. Ears should be in the water to listen for fish/mermaids.
- Can use the noodles. These are easier as they twist shape around the children's backs and fronts. She got the children to practice quite kicking.
- Asked the children to practice paddling. Paddling with arms, kicking and blowing bubbles.
Recommendations:
- When teaching it is easier to stand at the side. The children can swim in a circle. The instructor can make suggestions and changes to the swimmers techniques as they swim past in the circle.
- Some of my children were ready for back stroke. When teaching this it is "thumb up, pinky in, pull." Model this while standing facing the children and standing side on. This way they can see both sides clearly.
- It is also recommended to make the most of teaching swimming techniques outside if the pool. I could have children practicing the arm motion as a wee hotspot in the class. They could practice while walking over to the pool. They could also practice while waiting for their groups turn in the water.












No comments:
Post a Comment